G cannot be a constant
RELATIONSHIP OF MASS, RADIUS, AND TANGENTIAL VELOICITY"
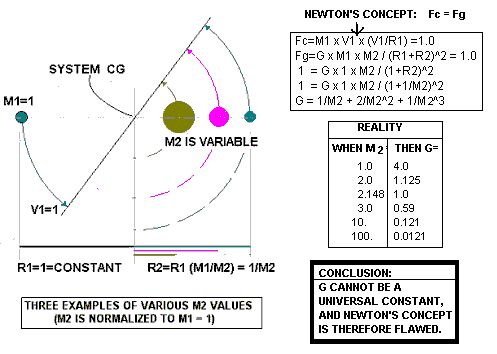
The illustration below depicts the orbital trace of celestial body M1 during mutual rotation about a common center of gravity with a second planet, M2. The mass and orbital path of M2 is depicted for three separate values of mass.All mathematical values for the mass, orbital radius, angular rate of rotation, and tangential velocity for M1 have been normalized to a value of 1.0 to simplify the mathematics. The corresponding values for the various selections of M2 are therefore measurable in terms of the ratio of M1/M2.
As indicated on the illustration, the mathematical value of G must vary in order for the 'centripetal' force which Newton imagined to exist to be equal to the actual value of centrifugal force which exists on the orbiting bodies in accord with the equation F=MV^2/R.
It should be pointed out that it was Newton himself who first recognized that if two celestial bodies are in mutual rotation, then they will rotate around their common center of gravity. Unfortunately, after that discovery, he apparently did not consider the affect on his prior postulations about mass attraction.
However, if Newton's universal constant, G, is truly constant, then it must follow that the distance between every pair of mutually rotating celestial bodies is the same. For example, it must follow that if G is a universal constant, then the Earth and Moon must be the same distance apart as the Earth and the Sun. That certainly is not in accord with our currently accepted understanding of astronomy.